Sumber: https:/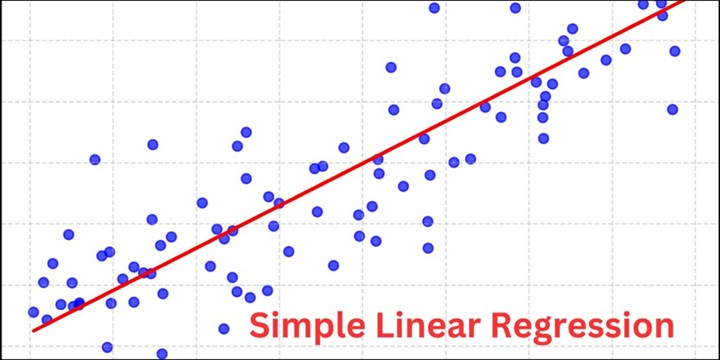/paravisionlab.co.in/simple-linear-regression-r/

Pernah melihat grafik garis lurus yang digunakan untuk memperkirakan harga, nilai ujian, atau tren masa depan? Itulah regresi linear sederhana—salah satu teknik prediksi paling mendasar dalam statistik. Dengan metode ini, kita dapat memahami bagaimana satu variabel memengaruhi variabel lainnya secara mudah dan sistematis.

1. Apa Itu Regresi Linear Sederhana?

Regresi linear sederhana adalah metode statistik untuk memprediksi nilai suatu variabel (Y) berdasarkan satu variabel lain (X).

📌 Inti dari regresi linear sederhana:

• Menggambarkan hubungan linear (garis lurus) antara X dan Y
• Menghasilkan model prediksi
• Menunjukkan seberapa besar pengaruh X terhadap Y

Regresi menjadi dasar banyak model dalam data science, machine learning, ekonomi, dan sains sosial.

2. Rumus Regresi Linear Sederhana

📌 Keterangan Rumus

• Y = variabel dependen (yang ingin diprediksi)
• X = variabel independen (yang memengaruhi Y)
• a = intercept → nilai Y saat X = 0
• b = slope → besar perubahan Y ketika X bertambah 1 unit

📌 Analogi Sederhana

• a = titik awal garis
• b = kemiringan garis (naik atau turun)

Jika b positif, hubungan meningkat.
Jika b negatif, hubungan menurun.

3. Contoh Kasus Nyata: Jam Belajar dan Nilai Ujian

Misalkan kita ingin melihat apakah jumlah jam belajar dapat memprediksi nilai ujian.

📊 Contoh Data Singkat

• 1 jam → nilai 60
• 2 jam → nilai 65
• 3 jam → nilai 70
• 4 jam → nilai 75

Jika hasil perhitungan menunjukkan:

Interpretasinya:

• 55 = nilai dasar saat tidak belajar sama sekali
• 5 = tambahan nilai untuk setiap 1 jam belajar

📌 Prediksi sederhana

Jika seorang siswa belajar 6 jam:

Dengan regresi, prediksi seperti ini menjadi mudah dilakukan.

4. Langkah-Langkah Melakukan Regresi Linear Sederhana

📌 1. Kumpulkan data X dan Y

Contoh: tinggi badan & berat badan, iklan & penjualan.

📌 2. Buat scatterplot

📍 Tujuan: melihat apakah pola hubungan terlihat linear.

📌 3. Hitung slope (b) dan intercept (a)

Biasanya menggunakan software seperti Excel, SPSS, Python, atau R.

📌 4. Bangun persamaan regresi

Persamaan ini menjadi alat prediksi.

📌 5. Evaluasi model

Gunakan metrik evaluasi (dibahas di bawah).

5. Mengukur Kualitas Model Regresi

📌 Koefisien Determinasi (R²)

Mengukur seberapa besar X menjelaskan variasi Y.

• R² = 0.7 → 70% variasi Y dijelaskan oleh X
• R² semakin tinggi berarti model semakin baik

📌 Standard Error

Mengukur rata-rata kesalahan prediksi.

📌 Uji Signifikansi (p-value)

Menilai apakah hubungan X dan Y benar-benar signifikan dan tidak terjadi karena kebetulan.

6. Kapan Regresi Linear Sederhana Cocok Digunakan?

Regresi linear sederhana cocok ketika:

• 🔹 Hanya ada satu variabel yang memengaruhi Y
• 🔹 Hubungan terlihat linear pada scatterplot
• 🔹 Tidak ada lonjakan outlier yang ekstrem
• 🔹 Data relatif homogen

📌 Contoh Penerapan dalam Kehidupan

• Ekonomi: memprediksi penjualan berdasarkan harga
• Kesehatan: memprediksi berat badan dari tinggi
• Pendidikan: memprediksi nilai ujian dari jam belajar
• Bisnis: memprediksi profit berdasarkan jumlah pelanggan

7. Kelebihan dan Keterbatasan Regresi Linear Sederhana

✨ Kelebihan

• Sangat mudah dipahami
• Cepat dihitung
• Visually interpretable (bisa digambar sebagai garis)
• Cocok untuk pemula dalam statistik

⚠ Keterbatasan

• Tidak menangkap pola non-linear
• Sangat sensitif terhadap outlier
• Tidak cocok untuk kasus dengan lebih dari satu variabel (solusi: regresi linear berganda)

Kesimpulan

Regresi linear sederhana adalah metode yang kuat namun mudah digunakan untuk memprediksi nilai berdasarkan satu variabel. Dengan memahami rumus dasar, interpretasi, dan cara mengevaluasi model, Anda dapat menggunakannya dalam banyak situasi analisis data. Ini merupakan fondasi penting sebelum melangkah ke metode yang lebih kompleks seperti regresi berganda atau model machine learning.

Referensi Singkat

• Montgomery, D. Applied Statistics and Probability for Engineers
• Wooldridge, J. Introductory Econometrics
• Tutorial statistik: Khan Academy & DataCamp