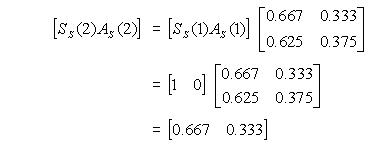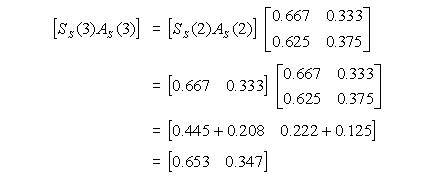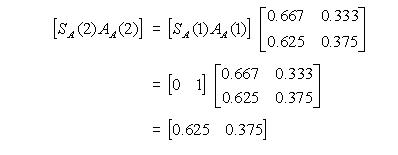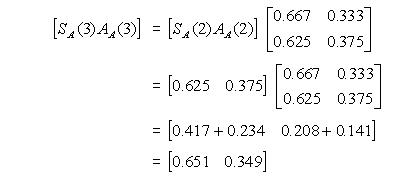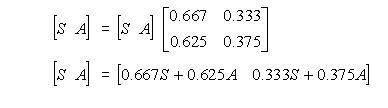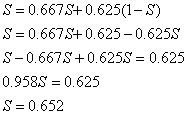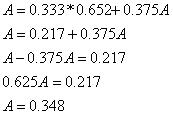Markov Chain
MARKOV CHAIN
Perubahan yang ada di dalam kehidupan sehari-hari sangat bervariasi. Ada perubahan yang bersifat statis namun ada juga yang bersifat dinamis. Karena kehidupan yang terus berjalan, maka perubahan yang terjadi memang tidak bisa dihindari. Acapkali perubahan itu juga berimbas pada sebuah kerugian. Oleh karena itu, ada baiknya apabila dilakukan persiapan untuk sebuah perubahan. Bagaimana caranya untuk menghadapi sebuah perubahan? Setiap transisi yang terjadi dari waktu ke waktu perlu dicermati dengan baik. Salah satu solusi yang relevan untuk situasi tersebut adalah dengan melakukan prediksi akan apa yang terjadi di masa yang akan datang.
Contoh perubahan:
– Prediksi perpindahan minat pada merk tertentu
– Manajemen pengobatan diabetes
– Pemantauan lalu lintas
Rantai Markov (Markov Chain) adalah sebuah teknik perhitungan yang umumnya digunakan dalam melakukan pemodelan bermacam-macam kondisi. Teknik ini digunakan untuk membantu dalam memperkirakan perubahan yang mungkin terjadi di masa mendatang. Perubahan-perubahan tersebut diwakili dalam variabel-variabel dinamis di waktu-waktu tertentu. Sehingga perlu untuk menyimpan nilai dari variabel keadaan pada tiap-tiap waktu tertentu itu
I. Sejarah Markov Chain
Model Rantai Markov ditemukan oleh seorang ilmuwan Rusia bernama Andrey Andreyevich Markov pada tahun 1906.
“Untuk setiap waktu t, ketika kejadian adalah Kt dan seluruh kejadian sebelumnya adalah Kt(j),…, Kt(j-n) yang terjadi dari proses yang diketahui, probabilitas seluruh kejadian yang akan datang Kt(j) hanya bergantung pada kejadian Kt(j-1) dan tidak bergantung pada kejadian-kejadian sebelumnya yaitu Kt(j-2), Kt(j-3), …, Kt(j-n)”
Gambar 1. Andrey Andreyevich Markov
Markov berfokus pada perluasan hukum bilangan besar dalam berbagai percobaan. Model ini berhubungan dengan suatu rangkaian proses dimana kejadian akibat suatu eksperimen hanya tergantung pada kejadian yang langsung mendahuluinya dan tidak tergantung pada rangkaian kejadian sebelum-sebelumnya yang lain.
II. Analisa Markov
Dalam kenyataannya, penerapan analisa Markov bisa dibilang cukup terbatas karena sulit untuk menemukan permasalahan yang memenuhi semua sifat yang diperlukan untuk analisa Markov, terutama persyaratan bahwa probabilitas transisi harus konstan sepanjang waktu.
Proses Markov Chain terdiri dari dua prosedur, yaitu menyusun matriks probabilitas transisi, dan kemudian menghitung kemungkinan market share di waktu yang akan datang. Probabilitas transisi adalah sebagai contoh pergantian yang mungkin dilakukan oleh konsumen dari satu merk ke merk yang lain. Konsumen dapat berpindah dari suatu merk ke merk yang lain disebabkan karena periklanan, promosi khusus, harga, ketidakpuasan, dan lain-lain. Hal ini akan bermanfaat karena jumlah market share-nya di periode yang akan datang akan bisa diperhitungkan sejak dini.
Metode ini banyak digunakan untuk pengambilan keputusan, namun sebenarnya hanya memberikan informasi bagi pengambil keputusan untuk memperbaiki keputusannya, bukan untuk memberi solusi.
Gambar 2. Rantai Markov
Langkah-langkah untuk menyelesaikan perhitungan probabilitas pada periode waktu tertentu menggunakan rantai Markov adalah sebagai berikut:
- Buatlah matriks transisi dari probabilitas yang diketahui
- Lakukan operasi perkalian matriks dari probabilitas waktu sebelumnya dengan matriks transisi. Rumusnya adalah: Matriks periode ke-n = Matriks periode ke-n+1 * Matriks transisi
- Ulang proses yang sama sampai menemukan probabilitas yang hendak dicari
Dalam perhitungan probabilitas yang terus berulang tersebut, akan ditemui pada periode tertentu bahwa probabilitas hasil perhitungan kedua matriks itu bernilai sama/tetap/tidak berubah apabila dihitung untuk periode-periode selanjutnya. Kondisi ini disebut dengan probabilitas keadaan tetap (steady state probability). Langkah yang dikerjakan untuk menemukan steady state probability adalah sama seperti langkah untuk menghitung probabilitas pada kondisi tertentu.
Nilai probabilitas pada periode-periode selanjutnya setelah bertemu dengan steady state probability ini akan sama. Karenanya, probabilitas ini bisa digunakan sebagai prediksi jumlah dalam keadaan tetap, dengan cara mengalikan steady state probability dengan jumlah orang yang terkait dengan permasalahan yang sedang dihadapi.
Permasalahan selanjutnya apabila perhitungan dilakukan per periode, tentunya akan memakan waktu yang lama, karena contohnya saja apabila steady state probability ada pada periode ke-15, maka harus dilakukan perhitungan sebanyak 14 kali. Hal ini bisa diatasi dengan menghitung probabilitas keadaan tetap secara langsung menggunakan persamaan.
Semua contoh perhitungan untuk semua penjelasan di atas bisa dilihat pada bagian Case Study di bawah ini.
III. Case Study
Suatu survei dilakukan di sebuah wilayah di kota Jakarta. Diketahui bahwa wilayah tersebut terdiri dari 1000 keluarga. Dari survei tersebut, diperoleh data bahwa 600 keluarga merupakan pelanggan toserba ‘Serba’ dan 400 keluarga merupakan pelanggan toserba ‘Ada’. Pada bulan itu, diketahui bahwa :
- Dari 600 keluarga pelanggan toserba ‘Serba’ diperoleh data bahwa 400 keluarga tetap berbelanja di toserba ‘Serba’ dan 200 lainnya berbelanja di toserba ‘Ada’.
- Dari 400 keluarga pelanggan toserba ‘Ada’ dinyatakan bahwa 150 keluarga tetap berbelanja di toserba ‘Ada’. Sedang 250 lainnya berbelanja di toserba ‘Serba’.
Hitunglah :
- Matriks probabilitas transisi untuk permasalahan di atas!
- Probabilitas untuk toko “Serba” dan “Ada” pada bulan ketiga apabila pada bulan pertama keluarga tersebut memilih untuk berbelanja di toko “Serba”
- Probabilitas untuk toko “Serba” dan “Ada” pada bulan ketiga apabila pada bulan pertama keluarga tersebut memilih untuk berbelanja di toko “Ada”
- Nilai probabilitas pelanggan dalam keadaan tetap!
- Jumlah perkiraan pelanggan dalam jangka panjang untuk masing-masing toserba tersebut!
Jawab:
a. Langkah pertama yang perlu dilakukan untuk menyelesaikan seluruh pertanyaan di atas adalah dengan menentukan matriks transisi untuk menghitung nilai probabilitas
- Probabilitas bulan pertama “Serba” dan bulan kedua “Serba” = 400/600 = 0.667
- Probabilitas bulan pertama “Serba” dan bulan kedua “Ada” = 200/600 = 0.333
- Probabilitas bulan pertama “Ada” dan bulan kedua “Serba” = 250/400 = 0.625
- Probabilitas bulan pertama “Ada” dan bulan kedua “Serba” = 150/400 = 0.375
Sehingga matriks transisi yang diperoleh adalah:
Keterangan:
Baris pertama kolom pertama : Bulan pertama “Serba”, bulan kedua “Serba”
Baris pertama kolom kedua : Bulan pertama “Serba”, bulan kedua “Ada”
Baris kedua kolom pertama : Bulan pertama “Ada”, bulan kedua “Serba”
Baris kedua kolom kedua : Bulan pertama “Ada”, bulan kedua “Ada”
b. Apabila pada bulan pertama, keluarga tersebut memilih untuk berbelanja di toko “Serba” artinya keluarga tersebut pasti memilih untuk berbelanja di toko “Serba”, jadi probabilitas keluarga tersebut datang ke toserba “Serba” adalah 1, dan probabilitas keluarga tersebut datang ke toserba “Ada” adalah 0.
Sehingga matriks probabilitas untuk bulan pertama adalah [ 1 0]
Apabila dilakukan perkalian antara matriks probabilitas pada bulan pertama dengan matriks transisi pada kasus ini maka akan diperoleh data:
Probabilitas pada bulan kedua yang diperoleh memiliki nilai yang sama dengan matriks transisi pada baris pertama. Tentu saja demikian, karena perhitungan yang dilakukan adalah matriks pada bulan pertama dengan matriks transisi yang dibentuk dari data probabilitas pada bulan kedua.
Kemudian, untuk menghitung probabilitas pada bulan ketiga adalah dengan mengoperasikan perkalian matriks antara matriks probabilitas bulan kedua dengan matriks transisinya. Sehingga diperoleh:
Jadi diperoleh probabilitas bulan ketiga, apabila pada bulan pertama memilih di toko “Serba”, untuk toserba “Serba” adalah 0.653, dan toserba “Ada” adalah 0.347.
NB: Ingat bahwa jumlah probabilitasnya harus selalu satu (1)
c. Apabila pada bulan pertama, keluarga tersebut memilih untuk berbelanja di toko “Ada” artinya keluarga tersebut pasti memilih untuk berbelanja di toko “Ada”, jadi probabilitas keluarga tersebut datang ke toserba “Ada” adalah 1, dan probabilitas keluarga tersebut datang ke toserba “Serba” adalah 0.
Sehingga matriks probabilitas untuk bulan pertama adalah: [1 0]
Apabila dilakukan perkalian antara matriks probabilitas pada bulan pertama dengan matriks transisi pada kasus ini maka akan diperoleh data:
Sedangkan untuk probabilitas bulan ketiga:
Jadi diperoleh probabilitas bulan ketiga, apabila pada bulan pertama memilih di toko “Ada”, untuk toserba “Serba” adalah 0.651, dan toserba “Ada” adalah 0.349
d. Menghitung probabilitas keadaan tetap bisa dilakukan dengan melakukan operasi perhitungan persamaan sebagai berikut:
Persamaan 1:
Persamaan 2:
Karena jumlah probabilitas adalah satu maka Persamaan 3:
Dari ketiga persamaan tersebut, kita substitusikan sehingga nilai probabilitas S dan A akan diperoleh. Probabilitas yang kita peroleh itulah yang merupakan probabilitas keadaan tetap.
Dari persamaan 3, maka bisa dikonversikan menjadi
Substitusikan ke persamaan 1:
Substitusikan hasil nilai S tersebut ke dalam persamaan 2:
Jadi probabilitas keadaan tetap (steady state) nya adalah:
Toserba “Serba” = 0.652
Toserba “Ada” = 0.348
e. Jumlah perkiraan pelanggan dalam jangka panjang bisa dihitung dengan mengalikan probabilitas keadaan tetap dengan jumlah total pelanggannya
Toserba “Serba” = 0.652 * 1000 = 652 pelanggan
Toserba “Ada” = 0.348 * 1000 = 348 pelanggan