Bagaimana Matematika Membantu Komputer Memahami Musik?
 Gambar 1. Musik
Gambar 1. Musik
Musik dan matematika sering dianggap sebagai dua dunia yang jauh berbeda. Musik dianggap penuh emosi dan kreativitas, sedangkan matematika identik dengan angka dan logika. Namun di era digital, keduanya justru saling terhubung sangat erat. Banyak teknologi musik—dari aplikasi tuning, software DAW, sampai algoritma chord recognition—bergantung pada konsep matematika.
Penelitian terbaru menunjukkan bahwa beberapa konsep matematika dasar seperti aritmetika modular dan regular expression dapat digunakan untuk menjelaskan cara komputer mengenali nada, memindahkan (transpose) lagu, hingga mengidentifikasi jenis-jenis chord. Artikel ini membahas bagaimana matematika membantu membangun algoritma yang membuat musik lebih mudah dianalisis secara digital.
Mengapa Musik Butuh Matematika?
Saat kita mendengar nada atau memainkan instrumen, otak kita mengenali pitch, interval, dan harmoni secara alami. Namun komputer tidak “mendengar” musik seperti manusia. Komputer membutuhkan cara formal untuk memahami apa itu C, G#, Bb, atau chord mayor.
Di sinilah matematika digunakan sebagai bahasa formal untuk menggambarkan:
- urutan nada dalam chromatic scale,
- perhitungan interval antar nada,
- perpindahan nada (transposition),
- pembentukan dan identifikasi chord,
- pola enharmonic equivalent seperti C# = Db.
Dengan bahasa matematika, konsep musik dapat diterjemahkan menjadi algoritma yang dapat dijalankan oleh komputer.
- Chromatic Scale dan Konsep Modular 12
Gambar 2. Nada dalam satu oktaf
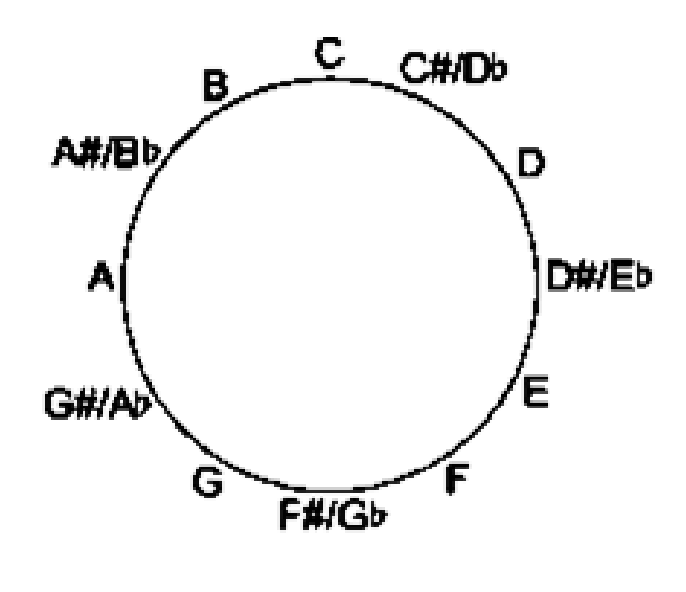
Dalam teori musik, satu oktaf terdiri dari 12 nada yang berulang. Setelah B, kita kembali ke C lagi. Struktur melingkar ini sangat cocok dijelaskan dengan aritmetika modular, khususnya modulo 12.
Misalnya, kita memberi indeks pada nada-nada berikut:
| Nada | C | C#/Db | D | D#/Eb | E | F | F#/Gb | G | G#/Ab | A | A#/Bb | B |
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Setelah indeks 11 (B), kita kembali ke 0 (C).
Matematikanya:
Konsep sederhana ini sangat penting untuk pemrograman musik.
- Mengapa Komputer Perlu “Regular Expression” untuk Nada?
Musisi tahu bahwa C# dan Db adalah nada yang sama. Tetapi bagi komputer, teks C# dan Db adalah dua string yang berbeda. Maka digunakanlah Regular Expression (regex)—sebuah pola pencocokan teks.
Contoh pola pencocokan untuk nada C# dan Db:
^(C#|Db)$
Dengan regex, komputer dapat mengenali:
- nada natural (C, D, E, …)
- nada dengan sharp (#)
- nada dengan flat (b)
- dan semua padanannya
Gambar 3. Simbol-simbol dalam Notasi Musik
Ini sangat membantu saat membuat sistem digital yang dapat menerima input musik dalam berbagai format.
- Transposisi Musik: Dari Rumus ke Algoritma
Transposisi adalah memindahkan nada atau seluruh lagu ke kunci lain. Ini biasa dilakukan oleh penyanyi atau pemain alat musik untuk menyesuaikan range mereka.
Dengan aritmetika modular, transposisi menjadi mudah. Misalnya, ingin memindahkan F ke atas 5 semitone:
- F = index 5
- 5 + 5 = 10
- index 10 = A#/Bb
Jika melampaui 11, komputer otomatis “melakukan wrap” kembali ke awal, sesuai sifat modulo.
- Menghitung Interval Antar Nada
Interval adalah jarak antara dua nada. Komputer dapat menghitung interval menggunakan perbedaan indeks:
Jika beda oktaf, tinggal ditambah kelipatan 12:
Dengan cara ini, komputer dapat menganalisis melodi, mencari pola, hingga mengenali genre berdasarkan karakter interval.
- Memahami Harmoni: Membentuk dan Mengenali Chord
Bagian paling menarik dari penelitian ini adalah bagaimana chord dapat dibangun dan diidentifikasi secara otomatis menggunakan matematika.
Setiap chord memiliki pola interval tertentu. Contohnya:
- Mayor: 0, 4, 7
- Minor: 0, 3, 7
- Diminished: 0, 3, 6
- Dominant 7: 0, 4, 7, 10
Dengan data interval tersebut, komputer dapat:
- Membentuk Chord dari Root Note
Misal C major:
- root = C (index 0)
- interval = 0, 4, 7
→ nada chord: C, E, GMengidentifikasi Chord dari Kumpulan Nada
Jika input = {E, G, C}, komputer:
- coba jadikan tiap nada sebagai root,
- hitung interval nada lain,
- cocokkan dengan pola interval chord.
Hasilnya: chord = C major.
Proses yang bagi manusia sangat cepat ini dapat direplikasi melalui algoritma matematis.
Kesimpulan
Musik digital tidak mungkin berkembang tanpa bantuan matematika. Penelitian ini menunjukkan bagaimana:
- aritmetika modular menjelaskan struktur nada,
- regular expression membantu komputer memahami notasi musik,
- perhitungan matematika dapat digunakan untuk transposisi, interval, dan harmoni,
- algoritma dapat membangun dan mengenali chord secara otomatis.
Pendekatan ini bukan hanya memperdalam pemahaman teori musik, tetapi juga membuka peluang besar untuk pengembangan teknologi audio, aplikasi edukasi musik, dan sistem komposisi otomatis di masa depan.
Penulis:
Kelvin Asclepius Minor, S.Kom., S.Si., M.Kom.
Referensi:
Rosen, K. H. (2019). Discrete Mathematics and Its Applications (8th ed.). McGraw-Hill Education.
Müller, M. (2015). Fundamentals of Music Processing: Audio, Analysis, Algorithms, Applications. Springer.
Loy, G. (2006). Musimathics: The Mathematical Foundations of Music, Volume 1. MIT Press.