Gambar 1. Machine Learning
Sumber: https://unsplash.com/illustrations/man-robot-and-binary-code-background-ai-singularity-digital-technologies-concept-vector-illustration-yaV_2X2l3bc

Machine learning mempunyai peran penting dalam perkembangan teknologi modern, mulai dari rekomendasi produk dan pemrosesan bahasa alami, hingga visi komputer dan sistem pendukung keputusan di berbagai sektor industri. Dalam perkembangannya, machine learning dapat digunakan di bidang keuangan untuk deteksi fraud dan penilaian risiko, di kesehatan untuk diagnosis berbasis citra dan prediksi progres penyakit, serta di logistik dan supply chain untuk peramalan permintaan dan optimasi jaringan distribusi. Namun di sisi lain, perkembangan machine learning memerlukan fondasi matematika yang kuat untuk merancang model yang tepat, memahami asumsi di balik algoritma, serta menjamin bahwa proses pelatihan dan prediksi berjalan stabil dan dapat dipercaya.

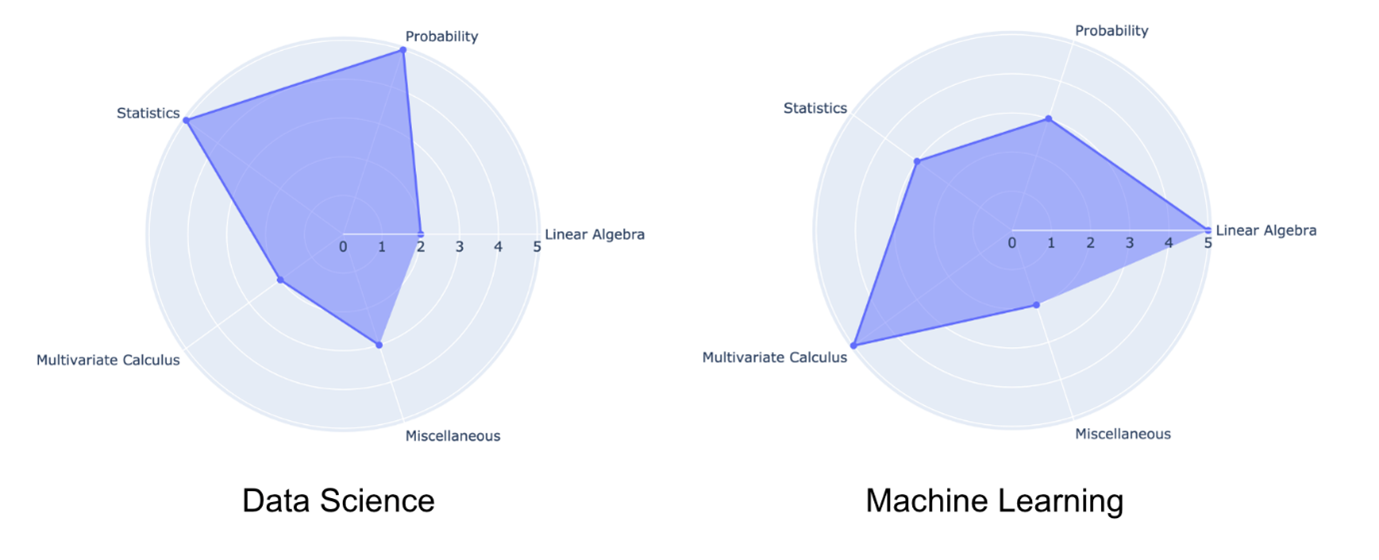
Gambar 2. Konsep Matematika dalam Data Science vs. Machine Learning
Sumber: https://www.analyticsvidhya.com/blog/2019/10/mathematics-behind-machine-learning/

Fondasi matematika tersebut mencakup aljabar linear sebagai bahasa untuk merepresentasikan data dan parameter dalam bentuk vektor dan matriks, geometri analitik untuk memaknai jarak, sudut, dan proyeksi di ruang berdimensi tinggi, serta dekomposisi matriks untuk mengungkap struktur laten seperti arah variasi terbesar dalam data. Di samping itu, kalkulus vektor menyediakan alat untuk menghitung gradien dan melakukan optimisasi fungsi objektif, sedangkan probabilitas dan statistika memberikan kerangka untuk memodelkan ketidakpastian, menyusun likelihood, dan melakukan inferensi terhadap parameter serta prediksi. Tanpa lapisan matematika ini, penggunaan machine learning cenderung menjadi “hit‑and‑run”: mencoba berbagai model seperti kotak hitam tanpa benar‑benar paham mengapa suatu pendekatan berhasil atau gagal.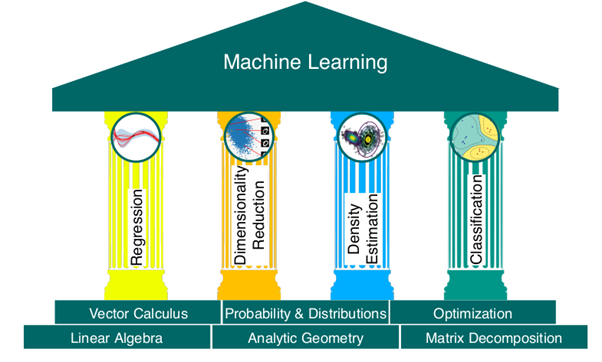

Gambar 3. Fondasi dan Empat Pilar Machine Learning
Sumber: https://www.analyticsvidhya.com/blog/2021/03/kickstart-guide-to-become-a-m-a-d-programmer/

Marc Peter Deisenroth dkk dalam bukunya Mathematics for Machine Learning mengajak pembaca menjembatani jurang antara matematika kuliah dasar dan algoritma machine learning yang banyak dipakai di praktik. Mereka menata kembali materi seperti sistem persamaan linear, ruang vektor, eigenvalue–eigenvector, turunan multivariat, distribusi Gaussian, hingga optimisasi kontinu, lalu memperlihatkan secara eksplisit bagaimana konsep‑konsep tersebut muncul dalam empat pilar ML: regresi linear, principal component analysis (PCA), Gaussian mixture models (GMM), dan support vector machines (SVM). Dengan pendekatan ini, pembaca tidak hanya belajar “cara menjalankan” algoritma, tetapi juga memahami struktur matematis yang mendasarinya, sehingga lebih siap untuk mengembangkan, memodifikasi, dan mengkritisi model‑model machine learning di dunia nyata.

Pada akhirnya, pesan utama buku tersebut adalah bahwa matematika bukan sekadar prasyarat yang harus dilalui sebelum belajar machine learning, melainkan alat berpikir yang membuat pembaca mampu merumuskan masalah dengan jernih dan menilai batas kemampuan model. Ketika seorang praktisi memahami bahwa regresi linear adalah proyeksi ke subruang, bahwa PCA adalah pencarian arah eigen utama, bahwa GMM adalah model probabilistik dengan variabel laten, dan bahwa SVM adalah solusi masalah optimisasi konveks dengan margin maksimum, maka machine learning berhenti menjadi kumpulan trik dan berubah menjadi disiplin yang koheren. Perspektif inilah yang menjadikan fondasi matematika bukan beban, tetapi investasi intelektual untuk membangun sistem machine learning yang lebih kuat, transparan, dan bertanggung jawab.

Penulis:
Dr. Alfi Yusrotis Zakiyyah, S.Pd., M.Si.=

Referensi

Deisenroth, M.P., Faisal, A.A. and Ong, C.S., 2020. Mathematics for machine learning. Cambridge University Press