Pola Rahasia Matematika Pembongkar Kepalsuan Dunia Maya
 Gambar 1. Sosial Media
Gambar 1. Sosial Media
Sumber: https://unsplash.com/illustrations/man-in-suit-falling-into-the-screeen-of-smartphone-which-looks-like-a-hole-social-media-addiction-and-depression-concept-vector-illustration-5cv_ZytSgxE
Seringkali kita merasa terpukau dengan angka likes yang fantastis, tanpa sadar bahwa itu hanyalah hasil rekayasa. Namun, sepandai apapun manipulasi itu, pemalsu data tidak akan bisa mengikuti secara persis pola angka yang muncul secara natural. Jadi, bagaimana matematika bisa membongkar kepalsuan yang ada di balik layar ponsel Anda?
Jawabannya terletak pada sebuah fenomena yang dikenal sebagai hukum Benford (Benford’s law). Sederhananya, hukum ini mengungkapkan bahwa secara natural data-data yang bersifat numerik —populasi kota, transaksi keuangan, atau jumlah teman di media sosial — akan memiliki pola yang khas: bilangan yang diawali dengan 1 muncul lebih sering (sekitar 30%), dan frekuensinya akan menurun drastis dari angka 1 ke angka 9. Hukum ini sudah menjadi golden standard untuk mendeteksi indikasi penipuan (fraud detection) karena satu alasan psikologis: manusia adalah pengarang angka acak yang buruk. Saat seseorang memalsukan data, mereka akan cenderung meratakan sebaran angka atau menghindari pola tertentu, yang justru membuat data melenceng jauh dari hukum Benford.
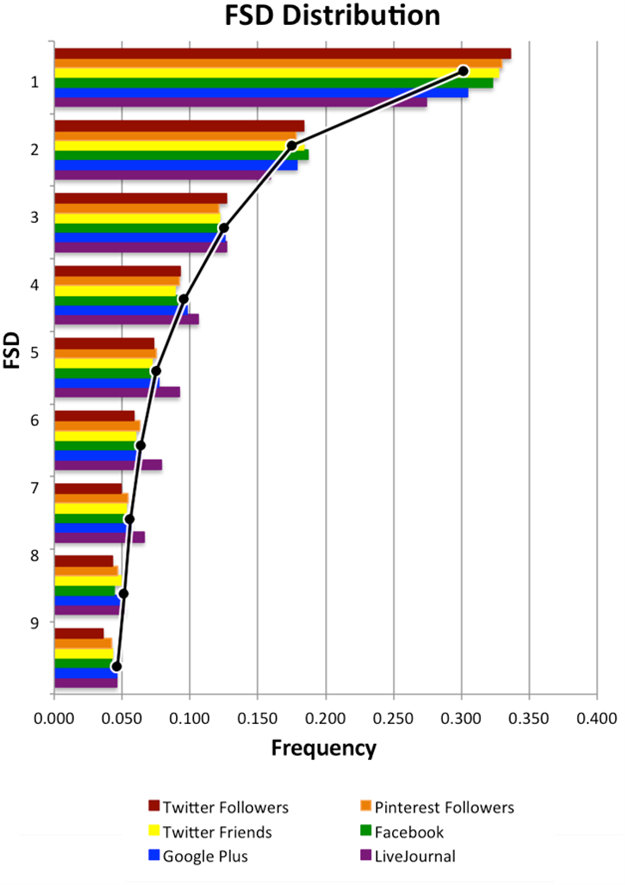
Gambar 2. Distribusi Digit Pertama (First Significant Digits) untuk banyak teman dan followers Twitter, Google Plus, Pinterest, Facebook, dan LiveJournal.
Sumber: Golbeck (2015)
Lantas, bagaimana penerapannya di dunia maya? Hal ini telah dikonfirmasi oleh berbagai penelitian, seperti studi dari Golbeck (2015) dan Bhosale & Di Troia (2022). Para peneliti menemukan bahwa akun pengguna manusia yang berinteraksi secara organik memiliki jaringan pertemanan yang sangat dinamis. Karena manusia bebas memilih siapa yang ingin mereka ikuti tanpa paksaan sistem, jumlah followers atau following mereka membentuk pola pertumbuhan alami yang luas. Menariknya, akumulasi angka-angka dari ribuan akun manusia ini secara kolektif akan membentuk kurva Benford dengan presisi yang sangat tinggi—sebuah bukti bahwa perilaku sosial kita yang bebas ternyata masih tunduk pada aturan matematika universal.
Sebaliknya, akun bot atau ‘pasukan siber’ hampir selalu gagal total dalam ujian statistik ini. Hal ini terjadi karena bot biasanya dikendalikan oleh instruksi program yang kaku. Misalnya, seorang penyedia jasa followers palsu mungkin menjalankan skrip yang memerintahkan 1.000 akun bot untuk masing-masing mengikuti tepat 50 atau 100 orang per hari agar tidak terdeteksi oleh sistem keamanan platform. Namun, keteraturan yang dipaksakan ini justru menjadi bumerang. Dalam analisis data, perilaku massal yang seragam ini akan menciptakan lonjakan tajam pada digit angka tertentu—misalnya angka 5 atau 1—dan menghancurkan kelandaian kurva Benford yang seharusnya turun dari angka 1 ke 9. Di sinilah matematika bekerja seperti lampu sorot yang mengungkap ‘ketidakwajaran’ di balik layar.
Gambar 3. Jumlah Likes
Sumber: https://unsplash.com/photos/black-and-brown-leopard-print-textile-5raGYibuitU
Fakta ini membawa pesan penting bagi kita di tengah riuhnya dunia maya. Angka-angka fantastis di layar—baik itu jumlah followers, likes, atau topik yang sedang tren—seringkali bukanlah cerminan suara publik yang nyata, melainkan ilusi hasil “ternak” algoritma. Memahami bahwa ada matematika yang mampu mengendus kepalsuan ini seharusnya membuat kita lebih kritis dan tenang: jangan biarkan validasi diri atau opini kita disetir oleh angka-angka yang bahkan tidak lulus uji statistik sederhana.
Pada akhirnya, matematika bukan sekadar pelajaran sekolah yang rumit, melainkan “detektif” yang paling jujur. Di dunia maya yang penuh topeng dan pencitraan, Hukum Benford mengingatkan kita bahwa kebenaran alami sangat sulit dipalsukan. Pembohong mungkin bisa memanipulasi persepsi manusia dengan jutaan likes palsu, tetapi mereka akan selalu kesulitan menipu semesta angka.
Penulis:
Rilo Chandra Pradana, S.Si., M.Kom.
Referensi:
- https://www.acfe.com/acfe-insights-blog/blog-detail?s=what-is-benfords-law-and-why-fraud-examiners-use-it
- Golbeck J (2015) Benford’s Law Applies to Online Social Networks. PLoS ONE 10(8): e0135169. https://doi.org/10.1371/journal.pone.0135169
- Bhosale, S., Di Troia, F. (2022). Twitter Bots’ Detection with Benford’s Law and Machine Learning. In: Bathen, L., Saldamli, G., Sun, X., Austin, T.H., Nelson, A.J. (eds) Silicon Valley Cybersecurity Conference. SVCC 2022. Communications in Computer and Information Science, vol 1683. Springer, Cham. https://doi.org/10.1007/978-3-031-24049-2_3