Topological Data Analysis (TDA): Seni Melihat “Bentuk” Asli Data

Pernahkah Anda mendengar teka-teki matematika bahwa cangkir kopi dan donat itu sebenarnya sama?

Ini bukan soal rasa atau bahan pembuatnya, melainkan tentang konsep matematika unik bernama Topologi. Dalam artikel ini, kita akan membahas bagaimana konsep “aneh” ini ternyata menjadi senjata ampuh dalam dunia data, yang dikenal sebagai Topological Data Analysis (TDA).

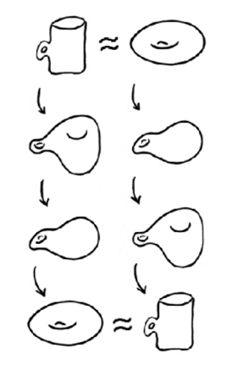
Homeomorfisme: Apa kesamaan dari cangkir dengan donat?

Bukan material atau hubungannya dengan makanan. Untuk memahami sifat unik Topologi, kita perlu berpikir abstrak, melampaui perspektif geometri. Dalam perspektif topologi: “Bentuk”nya yang sama! Berbeda dengan geometri, mempertimbangkan kesebangunan atau konruensinya. Dalam perspektif topologi, kesamaanya adalah, sama-sama sebuah objek geometri dengan 1 lubang yang disebut torus/donat.

https://www.youtube.com/watch?v=9NlqYr6-TpA&t=1s

Bentuknya dideformasi secara kontinu: bagian cangkir dibentuk dengan sedemikian rupa, sehingga cangkir menjadi donat. Sebaliknya juga berlaku, bisa dikembalikan bentuk semula, dari donat bisa menjadi cangkir lagi.

Konsep yang bisa dikembalikan ke bentuk semula disebut inversibilitas (Invers). Kesetaraan sifat antara objek cangkir dan objek donat disebut homeomorfisme, sama (homeo) + bentuk (morfis) atau “bentuk yang sama.” Bukan kongruensi geometris, tapi topological invariant.

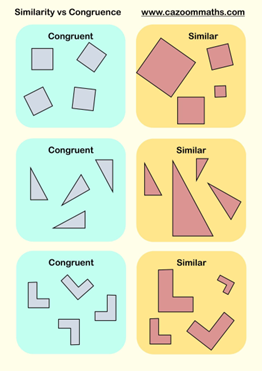
https://www.cazoommaths.com/teaching-resource/similarity-vs-congruent/

https://www.researchgate.net/figure/A-topological-transformation-of-a-donut-into-a-coffee-cup_fig14_326834755

Geometri objek yang kongruen (sudut dan panjangnya sama) akan dikatakan sama. Meskipun berbeda ukuran tapi jika sudutnya sama maka dikatakan sebangun. Jika sebuah objek yang sebangun/konruen ini, salah satu titiknya diubah jaraknya, yang menyebabkan sudutnya berubah, maka tidak dapat dikatakan sebangun/kongruen lagi.

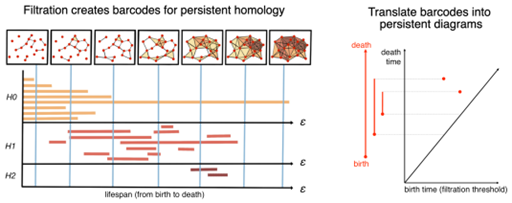
TDA memperhatikan invariant: lubang, keterhubungan, loops. TDA berfokus pada property/sifat yang dapat tidak berubah selama deformasi (topological invariant). Hal ini membuat sebuah bentuk data tahan terhadap noise, outlier, dll. Ketahanan ini dimungkinkan karena algoritma persistence homology, algoritma ini memastikan fitur topologi yang bertahan lama (persistence). Karena outlier akan menciptakan fitur topology yang kemunculannya singkat maka outlier akan terabaikan oleh algoritma persistence homology.

Berbicara tentang outlier, dalam kasus nyata bisa saja ada data yang terperncil. Hal ini karena data yang dikumpulkan tidak selalu ideal (sesuai distribusi statistik), di beberapa kasus bisa saja kesalahan input atau memang benar-benar fenomena langka.

Aplikasi lintas disiplin
Ketahanan TDA terhadap variasi bentuk, outlier, dll, sedang dikembangkan di berbagai bidang. Terutama yang memerlukan pemahaman mendalam tentang struktur/bentuk dari data, berikut 2 contoh bidang beserta aplikasinya:

  • Biomedical dan kedokteran
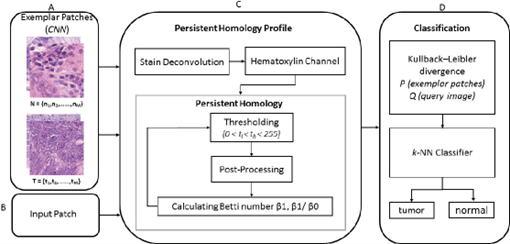
    TDA digunakan dalam dunia kedokteran untuk menganalisis data citra yang tidak ideal, noisy, outlier. Persistent Homology digunakan untuk segmentasi tumor dari gambar histologi, dalam sebuah studi algoritma mapper digunakan untuk mengidentifikasi 38 gen pembawa kanker dan dikonfirmasi menggunakan uji coba pada tikus [2].

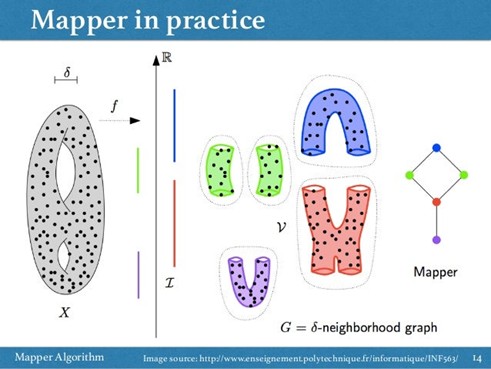
    Dalam sebuah paper metodological review [3], istilah/algoritma TDA diperkenalkan, yang menunjukan keilmuannya yang berdampak luas bahkan dalam bidang biomedical.
  • Image analysis

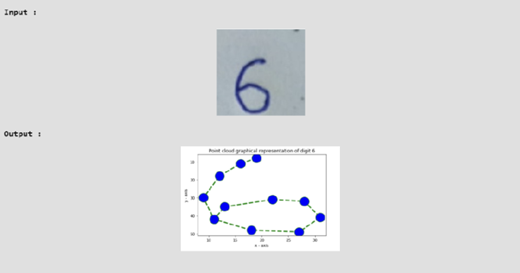
https://www.geeksforgeeks.org/data-science/hand-written-digits-using-topological-data-analysis/

Klasifikasi tulisan tangan, biasanya tulisan tangan memiliki variasi tinggi. Tulisan dapat memiliki kemiringan yang berbeda, bentuk yang lebih lancip, atau bentuk yang aneh tapi masih memiliki 1 lubang, selain itu barcode yang dihasilkan menggunakan persistence diagram bisa digunakan untuk mengenali huruf a yang tertutup dan juga yang sedikit terbuka.

Selain itu TDA digunakan untuk analisis struktur biokimia molekuler (protein folding) [4], ilmu material, analisis model 3D dalam bidang Biologi [5], atau Multivariate Time Series Analysis dalam bidang keuangan, prediksi cuaca [4] dll.

 

Kesimpulan

Kekuatan sejati TDA bukan hanya untuk menemukan fitur tersembunyi (loop, hole). Tetapi ketahanannya terhadap data yang tidak sempurna, bentuk yang berbeda secara geometris, outlier, dsb. Perspektif topologi ini lah, yang memberikan kita pandangan yang berbeda dan lebih abstrak dalam penarikan wawasan berbasis data (data analysis). Data tidak harus 100% berbentuk sama tapi bisa dengan kesamaan sifat/propertinya, bahwa data yang satu dan dengan data yang homeomorfis (mirip) dapat diduga memiliki kesamaan kasus, kesamaan penyelesaiannya, dll.

Penulis:
Tsui Tin Lun

Referensi:

[1] https://en.wikipedia.org/wiki/Topology

[2] https://pmc.ncbi.nlm.nih.gov/articles/PMC8076640/

[3] https://www.sciencedirect.com/science/article/pii/S1532046422000983

[4] https://www.linkedin.com/posts/anisht_topologicaldataanalysis-ai-datascience-activity-7368523086956056578-rb8D/

[5] https://pmc.ncbi.nlm.nih.gov/articles/PMC8511823/