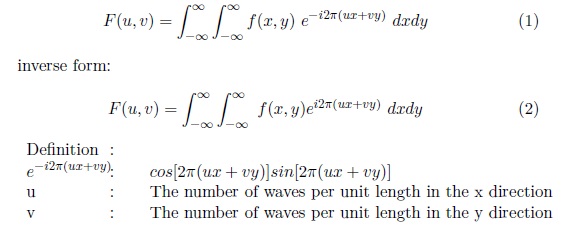Image Enhancement Using Frequency Domain Filtering

Fourier transform is used in the frequency domain for filtering. Fourier transform was introduced by the french mathematician Jean Baptiste Joseph Fourier.  His work was published in 1822 in his book, La Theorie Analitique  de la Chaleur. The main idea  behind  this  concept  is  any  signal  can  be broken down into a combination of simple waves. In details, any periodic function can be described as a summation of sines and/or cosines of different frequencies [1]. Here is a notation for 2d in fourier transform,

By converting spatial domain into frequency domain, some possible fil- ters can be used such as low pass, high pass, band pass and band stop filter. Out of four possibilities, low pass filter is used in this article.

In frequency domain, the center of the fourier image is the low frequency. By applying a filter such as in image 1c, means all frequency above cut off frequency are set to zero all frequencies above cut off frequency.  The last   step is to convert from frequency domain to spatial domain using inverse formula. In image 1d clearly shows that high frequency have been removed.

Bibliography

[1] Rafael C. Gonzalez; Richard E. Woods. Digital image processing third edition.  Pearson education international,  2008.