Self-Organizing Map (SOM)
Self-Organizing Map (SOM) atau sering disebut topology-preserving map pertama kali diperkenalkan oleh Teuvo Kohonen pada tahun 1996. SOM merupakan salah satu teknik dalam Neural Network yang bertujuan untuk melakukan visualisasi data dengan cara mengurangi dimensi data melalui penggunaan self-organizing neural networks sehingga manusia dapat mengerti high-dimensional data yang dipetakan dalam bentuk low-dimensional data. Metode pembelajaran yang digunakan SOM adalah tanpa bimbingan dari suatu data input-target atau unsupervised learning yang mengasumsikan sebuah topologi yang terstruktur menjadian unit-unit kelas/cluster (Kohonen, 1989 dan Fausett, 1993).
Pada algoritma SOM, vektor bobot untuk setiap unit cluster berfungsi sebagai contoh dari input pola yang terkait dengan cluster itu. Selama proses self-organizing, cluster satuan yang bobotnya sesuai dengan pola vektor input yang paling dekat (biasanya, kuadrat dari jarak Euclidean minimum) dipilih sebagai pemenang. Unit pemenang dan unit tetangganya (dalam pengertian topologi dari unit cluster ) terus memperbarui bobot merek (Fausett, 1993). Setiap output akan bereaksi terhadap pola input tertentu sehingga hasil Kohonen SOM akan menunjukkan adanya kesamaan ciri antar anggota dalam cluster yang sama.
Dalam jaringan SOM, neuron target tidak diletakkan dalam sebuah baris seperti layaknya model JST yang lain. Neuron target diletakkan dalam dua dimensi yang bentuk/topologinya dapat diatur. Topologi yang berbeda akan menghasilkan neuron sekitar neuron pemenang yang berbeda sehingga bobot yang dihaslkan juga akan berbeda. Pada SOM, perubahan bobot tidak hanya dilakukan pada bobot garis yang terhubung ke neuron pemenang saja, tetapi juga pada bobot garis ke neuron-neuron di sekitarnya. neuron di sekitar neuron pemenang ditentukan berdasarkan jaraknya dari neuron pemenang.
Arsitektur Topologi SOM
Arsitektur SOM merupakan jaringan yang terdiri dari dua lapisan (layer), yaitu lapisan input dan lapisan output. Setiap neuron dalam lapisan input terhubung dengan setiap neuron pada lapisan output. Setiap neuron dalam lapisan output merepresentasikan kelas (cluster )dari input yang diberikan.
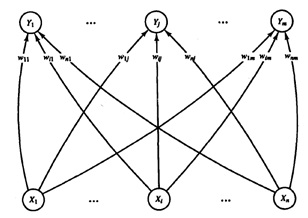
(Fausett, 1993)
Sedangkan untuk topologi, SOM memiliki 3 jenis topologi hubungan ketetanggaan (neighborhood) yaitu linear array, rectangular dan heksagonal grid.
Topologi linear aray menunjukkan cluster unit yang tersusun secara linear. Cluster unit yang menjadi pemenang [#] memiliki dua unit tetangga (neighbour) yang berjarak 1 (R = 1), dan mempunyai dua unit tetangga yang berjarak 2 (R = 2).
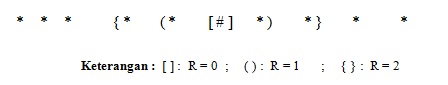
(Fausett, 1993)
Rectangular grid adalah topologi dari cluster unit dua dimensi. Unit tetangga (neighbour) dari unit pemenang membentuk bujur sangkar. Unit pemenang [#] memiliki 8 neighbour berjarak 1 (R=1) dan 16 neighbour berjarak 2 (R=2).
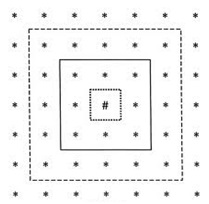
(Fausett, 1993)
Dalam topologi heksagonal grid, unit tetangga (neighbour) yang berjarak 1 (R=1) dari unit pemenang adalah 6 dan yang berjarak 2 (R=2) adalah 12.
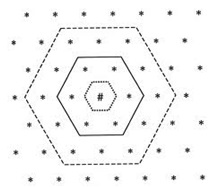
(Fausett, 1993)
Cara Kerja SOM
Secara umum, cara kerja SOM ditunjukkan oleh Gambar 5 dibawah ini:
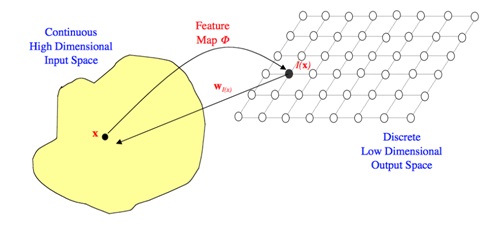
Terdapat titik (x) pada ruang input untuk dipetakan ke titik I(x) pada ruang output. Setiap titik (I) dalam ruang output akan memetakan ke titik yang sesuai dalam ruang input melalui bobot wI(x).
Menurut Haykin (1999) terdapat tiga komponen penting dalam SOM yaitu:
- Competition: Untuk setiap pola input, neuron menghitung nilai masing-masing fungsi diskriminan yang memberi dasar untuk kompetisi. Neuron tertentu dengan nilai terkecil dari fungsi diskriminan dinyatakan sebagai pemenang.
- Cooperation: Neuron pemenang menentukan lokasi spasial dari lingkungan topologi excited neuron untuk memberi dasar kerjasama dalam suatu lingkungan neuron.
- Synaptic Adaption: Excited neuron menurunkan nilai fungsi diskriminan yang berkaitan dengan pola input melalui penyesuaian bobot terkait sehingga respon dari neuron pemenang keaplikasi berikutnya dengan pola input yang sama akan meningkat.
Pustaka
Fausett. L.V (1993). Fundamental of Neural Network: Architectures, Algorithm, And Application. Prentice Hall, 1st edition. ISBN-13: 978-0133341867.
Haykin, S. (1999). Neural Networks: A Comprehensive Foundation. England: Pearson Education. Hal. 23, 43-45.
Kohonen, T (1989). “Self-organizing feature maps.” Self-organization and associative memory. Springer Berlin Heidelberg. 119-157.
Kohonen, T.,Schroeder, M. R and Huang, T (2001)Self-organizing map. Springer-Verlag New York. Inc., Secaucus, NJ, 43, 2.





