Part III. Collision Detection Phase

Collision Detection Phase is the moment where the game detects if there are any overlapping objects or not. (Thompson, 2005) Collision detection is divided into two phases: broad phase and narrow phase. Broad phase is performed before narrow phase.

Broad Phase

In the broad phase of collision physics for video games we need to identify which pairs of colliders might be colliding. These bodies might have complex shapes like polygons and polyhedrons, and what we can do to accelerate this is to use a simpler shape to encompass the object. If these bounding shapes do not intersect, then the actual shapes also do not intersect. If they intersect, then the actual shapes might intersect and further inspection is necessary (Souto, 2014). This phase usually followed by narrow phase but not always, some 2D arcade games only perform this phase. Broad phase strategy as we have found consists of several strategy options that developer can choose.

Dimension Reduction Strategy

The dimension reduction strategy or sort and sweep strategy considers each dimension one at a time. The endpoints of each object are projected onto each dimension and a check is done to see if any of the objects’ endpoints are overlapping. If a pair of objects has overlapping endpoints in all dimensions the pair is marked as possibly colliding. Figure 1 illustrates this for one dimension which is x axis projection. In the illustration, the pair containing BoundRect1 and BoundRect2 is a good candidate for collision detection because both x component of BoundRect2 and BoundRect1 are overlapping. On the other hand, neither object should be tested for collision with BoundRect3 and BoundRect4.

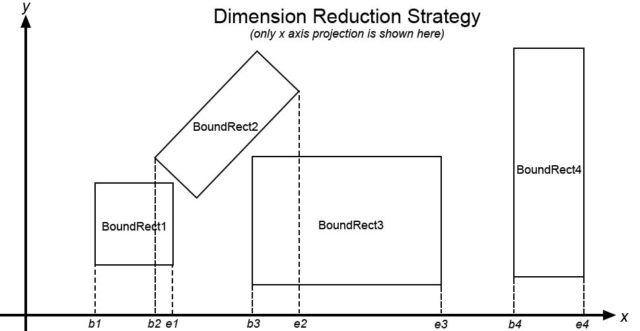
Dimension reduction strategy is also called sort and sweep strategy because we need to sort (by using any sorting algorithm) the beginning and ending of each BoundRect first and then sweep from the lowest value to the highest and see if there is any overlapping value of b (beginning) and e (ending). The value of beginning and ending of a BoundRect is taken from the lowest and highest of projection of its four corners to x or y axis. The algorithm continues to sweep both x and y axis. When the overlapping occurred for both x and y axis the pair are to be tested for narrow phase.

Axis-aligned Bounding Box

Axis-aligned Bounding Box or often known as AABB is a simple algorithm to detect bounding rectangle with another bounding rectangle where all sides of both rectangles are in aligned with axis of the coordinate system. This algorithm cannot be used for rectangle that is not in aligned with axis (e.g. rotated rectangle).

Dynamic Bounding Volume Trees

Another useful spatial partitioning method is the Dynamic Bounding Volume Tree, also known as DBVT. This is a type of Bounding Volume Hierarchy (BVH). The DBVT is a binary tree in which each node has an AABB that bounds all the AABBs of its children. The AABBs of the rigid bodies themselves are located in the leaf nodes. Typically, a DBVT is “queried” by giving the AABB for which we would like to detect intersections. This operation is efficient because the children of nodes that do not intersect the queried AABB do not need to be tested for overlap. As such, an AABB collision query starts from the root, and continues recursively through the tree only for AABB nodes that intersect with the queried AABB. The tree can be balanced through tree rotations similar to AVL tree balancing algorithm.(Souto, 2014) This type of strategy is suitable for video games that have only few moving objects and weak for a lot of dynamic objects because if lot of objects are often moving the tree must be often reconstruct again involving deletion, insertion and balancing.

Narrow Phase

In narrow phase we further inspect the collision in more detailed and precise way. This step can usually be skipped if broad phase is already sufficient for satisfying game rules and conditions. This algorithm is performed to further check whether a possible colliding objects that is detected in broad phase is really colliding or not. If the collided boundary object shape is not primitive (i.e. polygon), a further checking into polygonal level is necessary. This is done using polygon with polygon algorithm described before. If the object in game is drawn using raster-based image then there is an alternative algorithm that can inspect collision in detailed using Pixel Masking algorithm that will be described further.

Pixel Masking

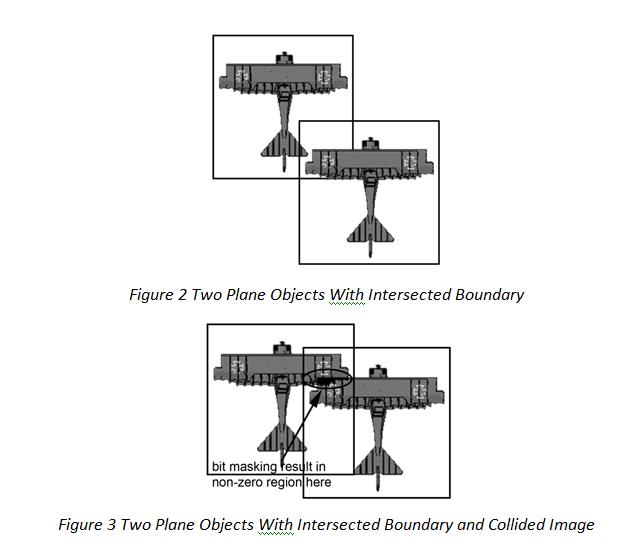
Pixel masking is an algorithm for accurately detecting collision of 2D objects. To use this algorithm the collider object drawing on screen must be based on image/raster (not vector/polygon based). The idea is to mask two images used by respective colliders using bitwise AND. If there is at least 1 bit active in the result of masking operation then a collision is confirmed otherwise no collision occurred. Figure 2 shows two plane objects in game that have their rectangle boundaries overlapped while actually they are still not collided. If we mask two images on Figure 2 using bit AND operator then there is no bit 1 found therefore the algorithm can accurately detect that there is no collision in Figure 2 case. While in Figure 3 we can see not only did the rectangle boundaries of both objects collided but also the masking result using bit AND operator results at least an active bit found (active bit means bit value = 1) in their masking image bit result.

Collision Detection Algorithm

A very common and trivial algorithm for collision detection would be as follow:

For each pair of colliders in game:

1. Set first collider as Collider1 and second collider as Collider2.
2. Calculate projected position of Collider1 and Collider2 given an interval time .
3. Check if boundary shape of projected Collider1 intersects/overlaps with boundary shape of projected Collider2.
4. If both boundary shapes overlap then collision exists and program enter Collision Resolve Phase to resolve this collision. If no overlap then both colliders can safely change their position to new position.

This naive algorithm will mostly cause problem described in Collision Detection Problem section. Also, because this algorithm is run every motion calculation period, it will perform very slow for a lot of colliders. It is slow because the complexity of algorithm is O(n²), checking collision with every possible combination of pair of colliders.

One suggestion of our optimized algorithm based on our experience is as follows.

1. Using one of several algorithms in broad phase, create a list of pair (list that contains many pairs of colliders) called PotCollideList. Add this PotCollideList with pairs of colliders that are possible to collide. PotCollideList now contains all pairs of colliders that are potential to collide.
2. If necessary (optional) continue to filter the potential pairs in PotCollideList with appropriate algorithm in narrow phase. After this step, PotCollideList contains a list of pairs that surely overlaps or touching.
3. For each element pair in PotCollideList, check if the pairs overlap, if so, resolve this overlapping condition by using collision response algorithm.
4. Determine the bounding motion of the object.
5. Calculate projected position of a rectangle
6. Calculate bounding motion rectangle
7. For each other bounding rectangle do check if bounding motion rectangle overlaps with another rectangle.
8. If there is an overlap then check where the collision is first made, if the collision exists resolve the collision using Collision Response Algorithm.

The restrictions for this algorithm are:

• It is only designed for rigid body, not soft body.
• It is only for 2D games.

Bibliography

Souto, N. (2014). Video Game Physics Tutorial. Retrieved 7 2016, from Toptal: https://www.toptal.com/game/video-game-physics-part-ii-collision-detection-for-solid-objects

Thompson, C. (2005). Building a 2D Physics Engine for MASON. George Mason University Department of Computer Science .