Deletion – AVL Tree
AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk tree dapat dipersingkat dan disederhanakan.
Ada 2 kasus yang biasanya terjadi saat operasi delete dilakukan, yaitu :
– Jika node yang akan dihapus berada pada posisi leaf atau node tanpa anak, maka dapat langsung di hapus.
- Jika node yang akan dihapus memiliki anak, maka proses penghapusannya harus di cek kembali untuk menyeimbangkan Binary Search Tree dengan perbedaan tinggi / level maksimal 1.
- anggap T adalah node yang harus diseimbangkan kembali
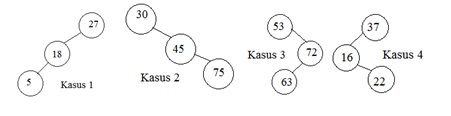
– Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
– Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
– Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
– Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)
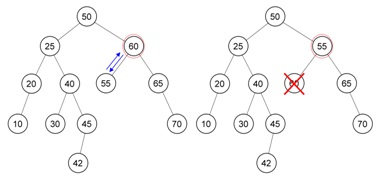
Berikut contoh dalam menghapus node AVL Tree, terdapat AVL Tree yang kemudian di hapus node 60. Dengan gambaran sebagai berikut :
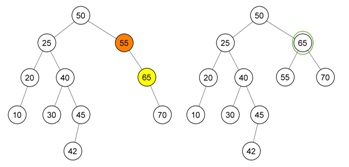
Yang akan menggantikan posisi node 60 adalah node 55. Akan terjadi ketidak seimbangan. Dengan tampilan sebagai berikut :
Maka akan dilakukan single rotation pada node 55 dengan kasus ketidak seimbangan pada kasus no. 2. Dengan tampilan setelah dilakukan single rotation sebagai berikut :
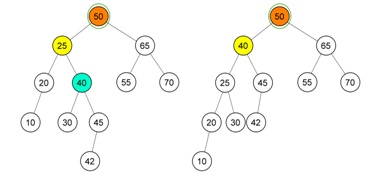
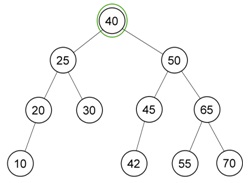
Ketika sudah dilakukan single rotation dan dilakukan kembali perbedaan tinggi / level maksimal 1 ternyata terdapat ketidak seimbangan yang terjadi. Sehingga diperlukan double rotation dengan kasus no. 4. Sehingga hasil dari rotasi yang dilakukan adalah sebagai berikut :
Rerefence :
Reema Thareja,. 2011. Data structures using C. OXFORD. New Delhi