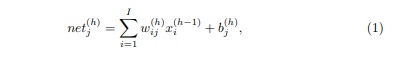ARTIFICIAL NEURAL NETWORK PART 3

1.3 Bobot,Kalkulasi Input dan Fungsi Aktivasi

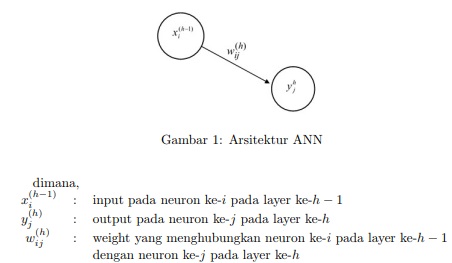
Dalam ANN, sinyal dari satu neuron ke neuron lain diberikan bobot (weight) yang pada awal proses, bobot-bobot ini akan ditentukan secara acak. Bobot adalah salah satu parameter yang sangat penting dalam proses penyelesaian masalah karena kesesuaian bobot yang digunakan menunjukan tingkat keberhasilan pembelajaran terhadap suatu pola yang akan dikenali. Dalam rangka penyesuaian bobot inilah maka dilakukan kalkulasi data-data pada input dengan bobot yang membawanya sehingga menghasilkan output yang sesuai dengan permasalahan yang akan diselesaikan. Dalam implementasi, arsitektur ANN yang digunakan pada umumnya akan terdiri dari beberapa layer yang merupakan representasi dari input, hidden dan output. Jika arsitektur ANN digambarkan sebagai(Gambar 1)[1];

sehingga kalkulasi kombinasi linear antara input dengan bobot dijumlahkan dengan bias dirumuskan dengan persamaan:

untuk j = 1, 2, …, l, dimana l adalah total jumlah neuron pada layer h. Hasil dari kombinasi linear ini akan menjadi input pada fungsi aktivasi yang dipilih. Fungsi aktivasi berperan untuk memberikan output pada setiap neuron, terdapat beberapa fungsi aktivasi yang dapat digunakan sesuai dengan masalah yang akan diselesaikan. Dengan tujuan untuk mempermudah pemahaman, maka jika dinotasikan,

maka fungsi-fungsi aktivasi dinyatakan sebagai:

1. Fungsi Linear
   
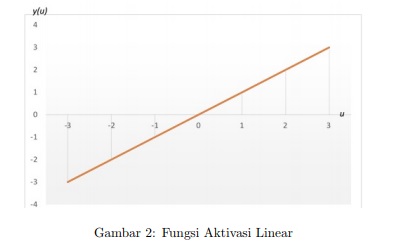
   Fungsi linear menghasilkan output yang sama dengan hasil kombinasi linear dan digambarkan pada Gambar 2 berikut
   
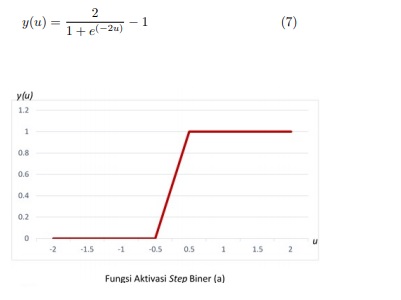
2. Fungsi Step,
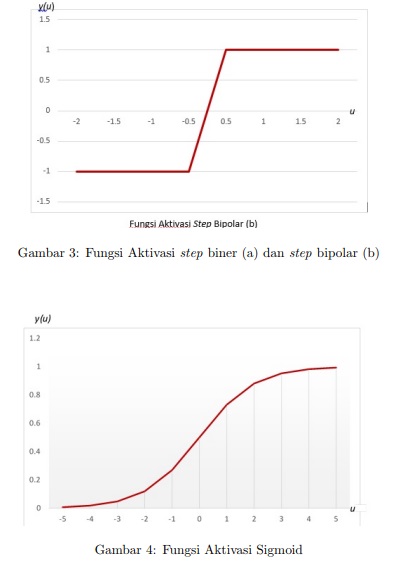
   Fungsi step terbagi atas 2, yaitu fungsi step biner atau dikenal juga sebagai fungsi hard limit dimana nilai output adalah;
   
3. Fungsi Sigmoid
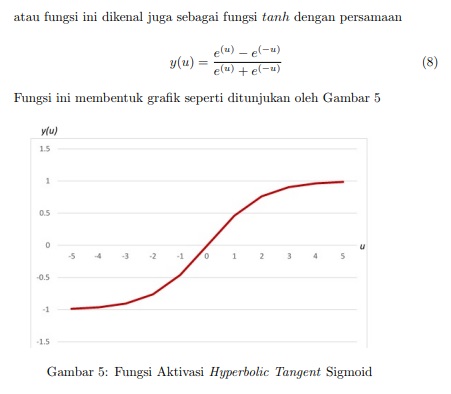
   Fungsi sigmoid digunakan untuk memperoleh output yang bersifat nonlinear, dirumuskan sebagai,
   
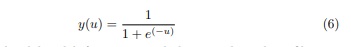
   Output yang dihasilakn oleh fungsi sigmoid akan membentuk grafik yang ditunjukan oleh Gambar 4
4. Fungsi Hyperbolic Tangent Sigmoid
   Hyperbolic Tangent Sigmoid memiliki persamaan
   
5. Fungsi Rectified Linear Unit (ReLU)
   Fungsi ReLU diperkenalkan oleh G.Hinton dan V.Nair pada tahun 2010 [2]. Fungsi ini digunakan pada kontex convolutional neural networks yang akan dibahas pada Bab 5. Fungsi ReLU dinyatakan dengan persamaan

   

6. Fungsi Gaussian
   Fungsi Gaussian memiliki persamaan
   
   
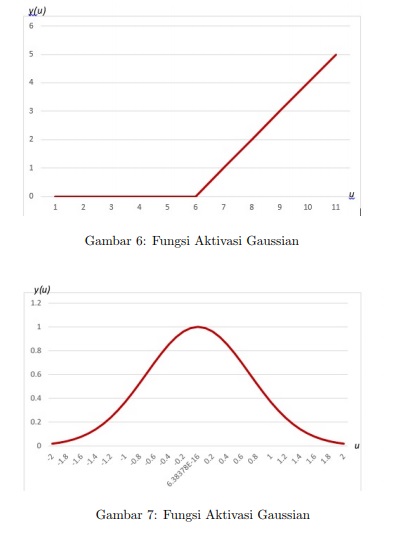
   yaitu hasil output pada neuron ke-j pada layer ke-h. Penggunaan fungsi aktivasi sangat bergantung pada permasalahan yang akan diselesaikan. Untuk kasuskasus linear penggunaan fungsi aktivasi step atau linear akan sangat efekti. Namun, untuk kasus-kasus nonlinear penggunaan fungsi sigmoid, tanh, ReLU ataupun Gaussian akan memberikan hasil yang baik. Nilai output yang menjadi target juga menjadi pertimbangan dalam pemilihan fungsi aktivasi. Sigmoid akan efektif digunakan jika target output memiliki interval nilai [0, 1], tanh untuk interval [−1, 1], Gaussian untuk interval (0, 1] dan ReLU untuk interval [0, ∞).