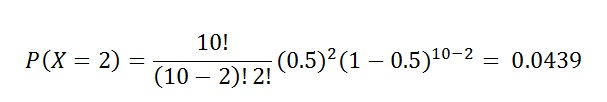DISTRIBUSI PELUANG BINOMIAL
BI dalam kata BINOMIAL berarti dua. Hal ini merujuk ke setiap kali percobaan atau kesempatan, hasil yang MUNGKIN muncul hanya ada dua.
Pertanyaan yang biasanya muncul adalah, kapan kita menggunakan menghitung peluang dengan menggunakan persamaan distribusi peluang Binomial? Jika kejadian tersebut memenuhi sifat-sifat di bawah ini maka ketika menghitung peluang kejadian tersebut terjadi maka persamaan yang digunakan adalah persamaan peluang dari distribusi binomial.
- Percobaan dilakukan sebanyak n kali.
- Setiap kali percobaan mempunyai dua kemungkinan hasil.
- Kemungkinan hasil dari masing-masing percobaan sama.
- Hasil yang diperoleh pada percobaan pertama tidak akan mempengaruhi hasil yang diperoleh pada percobaan-percobaan yang lain (saling independen).
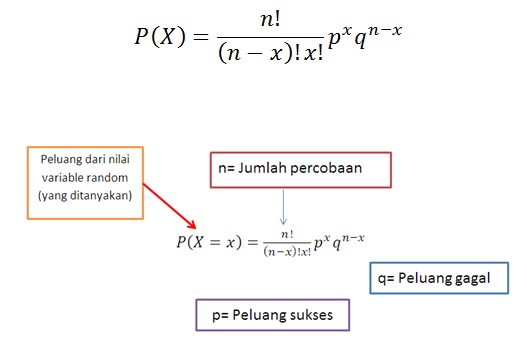
Untuk persamaan hitung peluang dapat dilihat sebagai berikut.
Misalkan X adalah variabel random diskrit. Maka peluang dari X adalah:
Contoh:
Misalkan kita mempunyai satu buah koin yang terdiri atas dua sisi, depan dan belakang. Misalkan kita mengundi sebanyak 10 kali. Pada undian pertama, kemungkinan hasilnya hanya sisi depan atau sisi belakang. Pada undian kedua, kemungkinan hasilnya hanya sisi depan atau sisi belakang. Demikian seterusnya. Setiap kali mengundi, kemungkinan hasilnya sama, hanya dua yaitu sisi depan atau sisi belakang. Dari sepuluh kali percobaan, berapa peluang sisi depan muncul sebanyak dua kali?
Diketahui:
Jumlah percobaan = n = 10.
Peluang sukses = peluang munculnya sisi depan dalam setiap percobaan = p = 0.5.
Peluang gagal = peluang tidak munculnya sisi depan dalam setiap percobaan = q = 1-p = 0.5.
Ditanyakan:
Dari sepuluh kali percobaan, berapa peluang sisi depan muncul sebanyak dua kali? Atau P (X = 2) -> Yang ditanyakan adalah peluang munculnya sisi depan maka kejadian yang dianggap sukses adalah jika sisi depan muncul ketika diundi.
Jawaban: