Cara Menghilangkan Left Recursive

Ketika menggunakan metode top-down parsing maka kita perlu menghilangkan left recursive dari grammar yang kita miliki. Penghilangan left recursive tidak akan mengubah makna dari aturan produksi tersebut, melainkan hanya memindahkan perulangan yang tadinya berada disebelah paling kiri dari aturan produksi yang ada ke sebelah paling kanan dari aturan produksi tersebut. Berikut adalah formula dari penghilangkan left recursive.

A -> Aα | β

Jika diberikan sebuah grammar produksi A yang memiliki aturan produksi Aα | β , dimana α bisa aturan apa saja namun diawali dengan variabel A (contoh Abc, Ac, dll.) dan β adalah aturan lainnya yang tidak mengandung left recursive (contoh bc, Bc, cA, dll.). Ketika kita ingin menghilangkan left recursive maka akan terbuat 1 variabel baru yaitu A’. Nama variabel yang baru bisa apa saja asalkan tidak sama dengan variabel pada CFG yang dimiliki. Formula dapat dilihat dibawah ini.

A -> βA’

A’ -> αA’ | ɛ

Lihatlah contoh berikut ini untuk mempermudah pemahaman dari formula tersebut. Diberikan sebuah CFG sebagai berikut:

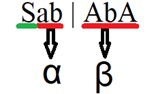
S -> Sab | AbA

A -> a | b

Dari grammar diatas kita tahu bahwa aturan produksi yang mengandung left recursive adalah yang S, sehingga kita perlu mencari yang mana adalah alpha dan beta.

Alpha adalah sisa aturan produksi yang didepannya mengadung variabel pemproduksi itu sendiri (memanggil dirinya sendiri yang terletak disebelah kiri dari grammar), sedangkan beta adalah aturan produksi yang tidak mengandung left recursive. Ketika menghilangkan left recursive maka grammar akan menjadi:

S -> AbAS’

S’ -> abS’ | ɛ

A -> a | b

Variabel produksi A akan tetap sama karena tidak mengandung left recursive.

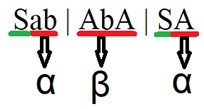
Contoh lainnya bila kita memiliki grammar S à Sab | AbA | SA , maka kita tahu bahwa ada 2 aturan produksi dari S ini yang mengandung left recursive, yaitu Sà Sab dan Sà SA. Alpha dari contoh kasus ini ada 2 yaitu ab dan A, sedangkan beta hanya 1 yaitu AbA.

Sehingga ketika kita menghilangkan left recursive maka akan menjadi sebagai berikut.

S -> AbAS’

S’ -> abS’ | AS’ | ɛ