Fast Fourier Transform (FFT) Penggerak Tersembunyi Teknologi Digital Masa Kini

Source: stock.adobe.com
Pendahuluan
Di kehidupan sehari-hari, kita dikelilingi oleh beragam bentuk data yang sejatinya merupakan sinyal, seperti suara manusia yang direkam melalui mikrofon, gambar digital yang tersusun dari titik-titik warna, sinyal listrik dalam perangkat medis, hingga transmisi data melalui jaringan nirkabel. Sebagian besar sinyal ini berubah terhadap waktu atau ruang dan sering kali sulit dianalisis secara langsung hanya dari bentuk aslinya. Untuk memahami isi dan struktur dari sinyal tersebut, para ilmuwan dan insinyur sering kali mengubahnya ke domain frekuensi, yaitu sebuah pendekatan yang memungkinkan kita melihat apa saja “nada”, pola periodik, atau struktur tersembunyi yang terkandung di dalam sinyal. Proses transformasi ini dilakukan menggunakan Transformasi Fourier, sebuah metode matematis yang dapat memecah sinyal kompleks menjadi kumpulan gelombang sinus sederhana.
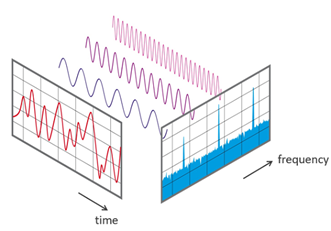
Source: nti-audio.com (2024)
Ketika data yang dianalisis berbentuk diskrit, seperti sampel digital dari sinyal audio atau pixel dalam gambar versi yang digunakan adalah Discrete Fourier Transform (DFT). DFT mengubah deretan angka digital menjadi representasi frekuensi dan ini sangat berguna dalam pemrosesan sinyal digital, analisis spektrum suara, kompresi data, bahkan dalam teknik pemodelan dan prediksi. Namun, meskipun DFT sangat kuat secara konseptual, ia memiliki satu kelemahan besar. Proses komputasinya sangat lambat untuk dataset berukuran besar karena setiap titik output membutuhkan perhitungan terhadap semua titik input, kompleksitas waktunya meningkat secara kuadratik, yakni sebesar di mana adalah jumlah sampel. Hal ini mengartikan bahwa semakin besar sinyal yang dianalisis, semakin tidak praktis penggunaan DFT dalam dunia nyata, terutama untuk aplikasi real-time seperti pemrosesan live audio, video streaming, atau sistem radar. Keterbatasan inilah yang mendorong lahirnya sebuah inovasi algoritmik revolusioner yang kita kenal sebagai Fast Fourier Transform (FFT). FFT bukan bentuk baru dari transformasi, melainkan metode cerdas untuk menghitung DFT secara lebih cepat. Dengan memangkas kompleksitas waktu dari menjadi hanya . FFT menjadikan analisis frekuensi dapat dilakukan secara efisien dan praktis, bahkan untuk sinyal berukuran besar sekalipun.
Sejarah Singkat FFT:
Meskipun FFT sering dikaitkan dengan publikasi James Cooley dan John Tukey pada tahun 1965, ide dasar dari algoritma ini sebenarnya sudah lama ditemukan. Versi awalnya bahkan pernah digunakan oleh Carl Friedrich Gauss pada tahun 1805 untuk menghitung orbit asteroid menggunakan metode interpolasi trigonometri. Namun, pada masa itu, belum ada perangkat komputasi digital yang mampu mengaplikasikannya secara luas. Barulah pada sekitar tahun 1960-an, ketika kebutuhan akan pemrosesan sinyal cepat muncul dalam konteks militer, eksplorasi luar angkasa, dan telekomunikasi algoritma ini dihidupkan kembali. Cooley dan Tukey memperkenalkan metode pemfaktoran sinyal menjadi blok-blok kecil dan menggabungkannya kembali menggunakan sifat periodisitas dan simetri dari eksponensial kompleks, yang menghasilkan versi FFT paling terkenal hingga kini, yaitu algoritma radix-2 Cooley–Tukey FFT (Cooley & Tukey, 1965). Kecepatan FFT yang signifikan menjadikannya salah satu terobosan paling berpengaruh dalam sejarah algoritma numerik (Frigo & Johnson, 2005).
Cara Kerja FFT:
FFT menghitung DFT melalui pendekatan divide and conquer. Alih-alih menghitung semua perhitungan DFT secara langsung, FFT membagi sinyal ke dalam bagian genap dan ganjil serta menghitung DFT dari masing-masing bagian secara rekursif. Hasilnya kemudian digabungkan kembali dengan memanfaatkan twiddle factor, yaitu rotasi kompleks yang menggambarkan perubahan fase. Twiddle factor dirumuskan sebagai dan berfungsi sebagai pengimbang rotasi antara hasil DFT genap dan ganjil, agar hasil akhirnya tepat berada pada frekuensi yang sesuai.
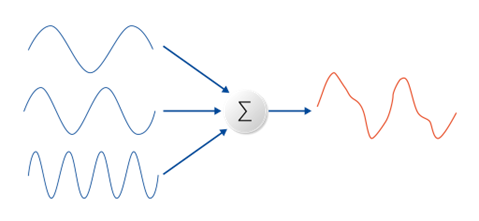
Source: svantek.com (2024)
Proses rekursif ini sangat efisien karena FFT hanya memerlukan tahap pembagian. Misalnya, jika kita memiliki sinyal berukuran 8 titik (N = 8), maka algoritma akan membaginya menjadi dua DFT dari 4 titik, kemudian menjadi empat DFT dari 2 titik, hingga delapan DFT dari 1 titik. Jumlah total operasinya kira-kira hanya 24, dibandingkan dengan 64 operasi pada DFT biasa. Hal inilah yang membuat mengapa FFT menjadi jauh lebih cepat dibandingkan metode DFT langsung. Pendekatan ini menghasilkan struktur berbentuk pohon rekursif. Setiap level memecah masalah menjadi bagian-bagian yang lebih kecil dan ketika digabungkan kembali dengan bantuan twiddle factor, kita mendapatkan hasil akhir DFT dengan efisiensi tinggi. Proses ini tidak hanya mengurangi waktu komputasi, tetapi juga membuat FFT dapat digunakan dalam sistem real-time.
Untuk memberikan gambaran lebih konkret tentang dampaknya, perhatikan tabel berikut yang memperbandingkan kebutuhan operasi antara DFT dan FFT untuk berbagai ukuran sinyal:
| Ukuran Sinyal () | Operasi DFT | Operasi FFT |
| 8 | 64 | 24 |
| 1.024 | 1.048.576 | 10.240 |
| 16.384 | 268.435.456 | 196.608 |
Efisiensi komputasi yang drastis inilah yang membuat FFT menjadi algoritma fundamental dalam pemrosesan sinyal digital modern. Ia memungkinkan analisis frekuensi dilakukan secara cepat dan akurat, bahkan untuk data berukuran sangat besar, serta membuka jalan bagi kemajuan teknologi komunikasi, multimedia, dan kecerdasan buatan.
Dampak FFT dalam Dunia Nyata:
- Pemrosesan Audio
FFT digunakan untuk menghasilkan spectrogram, menghapus noise, mendeteksi pitch, atau membuat efek suara. Kompresi seperti MP3 mengandalkan transformasi domain frekuensi agar bisa membuang informasi yang tidak terdengar oleh telinga manusia.
- Kompresi Gambar dan Video
Format seperti JPEG dan MPEG menggunakan transformasi serupa FFT untuk mengubah blok pixel menjadi frekuensi dan membuang detail yang tidak penting secara visual.
- Telekomunikasi
Dalam sistem seperti Orthogonal Frequency Division Multiplexing (OFDM) yang digunakan di 4G dan 5G, FFT digunakan untuk memisahkan data ke dalam sub-frekuensi yang berbeda secara simultan dan efisien.
- Medis dan Sains
Dalam pencitraan medis seperti MRI, FFT digunakan untuk membangun kembali gambar tubuh dari data sinyal elektromagnetik. Di dunia ilmiah, FFT mempercepat simulasi getaran, gelombang, bahkan dalam pengolahan genomik.
- Deep Learning dan AI
FFT membantu mempercepat training model, terutama dalam audio classification, voice recognition, dan pengolahan data spektral. Banyak model CNN untuk audio memakai spectrogram berbasis FFT sebagai input utama.
Penutup
Fast Fourier Transform (FFT) bukan sekadar algoritma percepatan, melainkan representasi dari bagaimana formulasi matematis yang efisien dapat mengatasi keterbatasan komputasi dalam pengolahan sinyal. Melalui pendekatan divide and conquer, FFT berhasil memangkas kompleksitas komputasi dari menjadi , menjadikannya jauh lebih layak digunakan dalam berbagai aplikasi real-time dan skala besar. Inovasi ini secara fundamental memperbaiki cara kita mengakses informasi dalam domain frekuensi, yang sebelumnya mahal secara komputasi melalui DFT. Keunggulan FFT tidak hanya terletak pada efisiensi algoritmiknya, tetapi juga pada fleksibilitas penerapannya di berbagai bidang. Dalam pemrosesan audio, video, komunikasi digital, sistem radar, pencitraan medis, hingga sistem pembelajaran mesin modern, FFT menjadi komponen inti yang memungkinkan proses transformasi sinyal berlangsung secara cepat dan akurat. Dalam konteks ini, FFT telah menjadi tulang punggung dari banyak teknologi yang hari ini dianggap sebagai standar, bahkan tanpa disadari oleh penggunanya.
Dengan demikian, FFT merupakan pencapaian penting dalam evolusi ilmu komputer dan teknik. Ia menunjukkan bagaimana prinsip-prinsip matematis klasik dapat diadaptasi dan diimplementasikan secara efektif untuk menjawab tantangan teknologi modern. Ke depan, meskipun terus bermunculan pendekatan baru dalam pemrosesan sinyal dan data, keberadaan FFT tetap relevan sebagai solusi yang terbukti efisien, teruji secara ilmiah, dan mendasar dalam fondasi sistem digital saat ini.
Penulis
Satriadi Putra Santika
FDP Scholar
Daftar Pustaka
Cooley, J. W., & Tukey, J. W. (1965). An algorithm for the machine calculation of complex Fourier series. Mathematics of Computation, 19(90), 297–301. https://doi.org/10.2307/2003354.
Svantek. (2024). FFT Fast Fourier Transform. https://svantek.com/academy/fft-fast-fourier-transform/. Di akses 29 Juni 2025.
NTI Audio. (2024). Fast Fourier Transformation FFT – Basics. https://www.nti-audio.com/en/support/know-how/fast-fourier-transform-fft. Di akses 29 Juni 2025.
Frigo, M., & Johnson, S. G. (2005). The design and implementation of FFTW3. Proceedings of the IEEE, 93(2), 216–231. https://doi.org/10.1109/JPROC.2004.840301.
Maklin, C. (2024). Fast Fourier Transform Explained. https://builtin.com/articles/fast-fourier-transform. Di akses 29 Juni 2025.


