Kompleksitas Algoritma: Seni Mengukur Efisiensi Sebuah Solusi
Pernahkah Anda merasa ada dua cara berbeda untuk mencapai tujuan yang sama? Misalnya, mencari alamat rumah teman. Cara pertama, Anda cek peta satu per satu hingga ketemu. Cara kedua, Anda langsung gunakan GPS yang memberikan jalur tercepat. Keduanya bisa sampai, tetapi jelas yang satu lebih efisien.
Hal yang sama terjadi dalam dunia komputer. Saat menyelesaikan masalah—seperti mencari data dalam daftar, mengurutkan ribuan nama, atau menghitung rute terpendek—bisa ada banyak algoritma berbeda. Pertanyaan pentingnya: mana yang lebih cepat, lebih hemat, dan lebih efisien?
Di situlah kompleksitas algoritma berperan.
Apa Itu Kompleksitas Algoritma?
Kompleksitas algoritma adalah ukuran seberapa efisien sebuah algoritma dalam menggunakan sumber daya. Biasanya, yang diukur ada dua:
- Kompleksitas Waktu (Time Complexity)
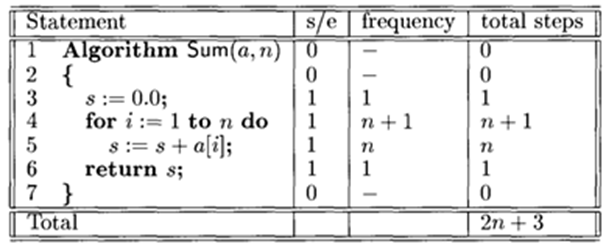
- Mengukur berapa banyak langkah yang diperlukan algoritma seiring bertambahnya ukuran input.
- Misalnya, berapa lama waktu yang dibutuhkan untuk mengurutkan 10 nama dibanding 1 juta nama.
- Kompleksitas Ruang (Space Complexity)
- Mengukur berapa banyak memori tambahan yang dibutuhkan algoritma.
- Contohnya, algoritma rekursif yang menyimpan banyak “jejak panggilan” biasanya butuh memori lebih besar dibanding algoritma iteratif.
Bahasa Universal: Notasi Big-O
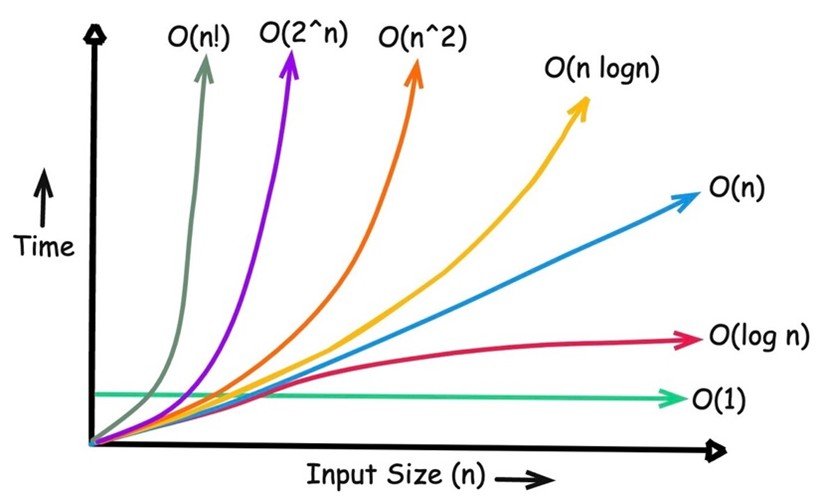
Untuk menuliskan kompleksitas, para ilmuwan komputer menggunakan notasi Big-O.
- O(1) – Konstan
Waktu eksekusi tidak berubah meski input bertambah.
👉 Contoh: Mengakses elemen ke-5 dari array. - O(log n) – Logaritmik
Waktu bertambah pelan meski input sangat besar.
Contoh: Binary Search pada daftar terurut. - O(n) – Linear
Waktu bertambah sebanding dengan ukuran input.
Contoh: Mencari angka terbesar dalam daftar dengan mengecek semua elemen. - O(n log n)
Masih relatif efisien meski data besar.
Contoh: Algoritma pengurutan seperti Merge Sort atau Quick Sort. - O(n²) – Kuadratik
Waktu melonjak drastis ketika input membesar.
Contoh: Bubble Sort, Selection Sort. - O(2^n) atau O(n!) – Eksponensial/Faktorial
Sangat tidak efisien, hanya cocok untuk input kecil.
Contoh: Brute-force pada masalah Traveling Salesman.
Analogi Sehari-Hari
Supaya lebih mudah, mari bayangkan dalam konteks kehidupan nyata:
- O(1): Membuka pintu rumah dengan kunci. Selalu satu langkah, tak peduli rumah Anda punya 1 atau 100 kamar.
- O(n): Mengecek daftar belanja untuk menemukan satu item. Semakin banyak daftar, semakin lama.
- O(n²): Membandingkan setiap orang di sebuah pesta dengan semua orang lainnya. Jika ada 100 orang, ada 10.000 perbandingan!
- O(log n): Mencari nama di kamus dengan teknik “buka di tengah”. Anda tak perlu membaca semua halaman.
Dengan analogi ini, kompleksitas bukan lagi angka-angka membingungkan, melainkan “cara kita menghitung usaha yang dibutuhkan.”
Mengapa Kompleksitas Itu Penting?
Bayangkan sebuah aplikasi e-commerce dengan jutaan produk. Jika algoritma pencarian menggunakan metode O(n²), pengguna harus menunggu lama untuk menemukan barang yang diinginkan. Aplikasi jadi lambat, bahkan bisa gagal melayani saat trafik tinggi.
Alasan mengapa kompleksitas penting:
- Efisiensi – Algoritma yang buruk bisa membuat komputer super cepat sekalipun menjadi lamban.
- Skalabilitas – Program yang efisien bisa tetap berjalan baik meski data membesar.
- Penghematan Biaya – Sumber daya komputasi adalah biaya nyata. Semakin hemat, semakin murah operasional.
- Kepuasan Pengguna – Tidak ada yang mau menunggu aplikasi loading terlalu lama.
Contoh Nyata dalam Dunia Komputer
- Mesin Pencari Google: Algoritma pencarian harus memproses miliaran halaman. Kompleksitas algoritma pencarian dan pengindeksan yang efisien sangat menentukan kecepatan hasil yang kita nikmati.
- E-commerce: Fitur “produk terkait” atau “rekomendasi” melibatkan algoritma kompleks. Efisiensi menentukan apakah hasil bisa muncul dalam 1 detik atau 10 detik.
- Aplikasi Navigasi (Google Maps/Waze): Menghitung rute tercepat membutuhkan algoritma graf (seperti Dijkstra). Kompleksitas menentukan apakah aplikasi bisa memberi rute real-time atau tidak.
Studi Kasus: Mencari Angka Terbesar
Misalnya kita punya daftar 1 juta angka, dan ingin mencari angka terbesar:
- Cara 1: Linear Search
Bandingkan semua angka satu per satu.
Kompleksitas: O(n) – relatif cepat dan efisien. - Cara 2: Urutkan lalu ambil angka terakhir
Urutkan seluruh data dengan algoritma pengurutan.
Kompleksitas: O(n log n) – lebih lambat, padahal kita hanya perlu angka terbesar, bukan semua urutan.
Dari sini terlihat, algoritma yang lebih “pintar” bisa jauh menghemat waktu dan sumber daya.
Kesimpulan
Kompleksitas algoritma adalah ilmu untuk mengukur efisiensi solusi komputasi. Ia membantu kita memilih algoritma yang tidak hanya menghasilkan jawaban benar, tapi juga melakukannya dengan cepat dan hemat sumber daya.
Seiring dunia bergerak menuju big data dan AI, kompleksitas algoritma semakin penting. Algoritma yang efisien dapat menjadi pembeda antara aplikasi yang sukses dipakai jutaan orang, atau aplikasi yang ditinggalkan karena terlalu lambat.
Penulis :
Fiqri Ramadhan Tambunan, S.Kom., M.Kom – FDP Scholar
Referensi
- Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms (3rd ed.). MIT Press.
- Levitin, A. (2012). Introduction to the Design and Analysis of Algorithms. Addison-Wesley.
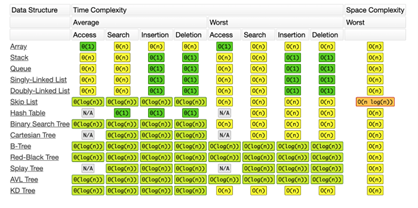
- Big-O Cheat Sheet. https://www.bigocheatsheet.com
- GeeksforGeeks – Analysis of Algorithms. https://www.geeksforgeeks.org/fundamentals-of-algorithms
- Khan Academy – Intro to Big-O Notation. https://www.khanacademy.org/computing/computer-science/algorithms/asymptotic-notation/a/big-o-notation


